Факторный анализ: основные положения и ошибки применения

В.П. Леонов

Сокращённая версия статьи опубликована в
"Международном журнале медицинской практики"
(вып.3, 2005, стр. 14-16).

ФАКТОРНЫЙ АНАЛИЗ (от лат. factor - действующий, производящий и греч. analysis - разложение, расчленение) - совокупность методов, которые на основе объективно существующих корреляционных взаимосвязей признаков (или объектов) позволяют выявлять латентные (или скрытые) обобщающие характеристики структуры изучаемых объектов и их свойств.

Многомерные методы постепенно входят в практику статистического анализа биомедицинских данных. Зарубежные исследователи используют их примерно в 30% публикаций, тогда как в российских публикациях их доля минимальна. Однако во многих из таких публикаций метод используется с разнообразными нарушениями, вследствие которых авторские выводы не всегда корректны. Цель нашей публикации кратко перечислить основные цели этого вида статистического анализа, а также рассказать о наиболее популярных ошибках его использования. Данная статья не является учебным пособием по теории факторного анализа (ФА), и тем более, учебным пособием по реализации этого метода в том или ином статистическом пакете. На эту тему есть специальные книги, имеющие объём несколько сот страниц.

Попытки использовать математику, и статистику в частности, в биомедицине имеют давнюю историю. Однако до сих пор язык математики не стал для врачей столь же привычным и необходимым, как, например, для инженера или физика. В чём основная причина этого явления? На наш взгляд основная причина этого не в том, что биомедицина еще «не дозрела» для такого «брака по любви (расчёту?)». Напротив, можно говорить о том, что биомедицина по своему содержанию гораздо сложнее тех наук, откуда пришло большинство математических идей и методов. Общеизвестно, что развитие большинства математических методов «оплодотворялось» насущными потребностями таких наук, как механика, физика, электротехника и т.д. По этой причине «точные науки» и поныне сохраняют эти связи и математический язык, нежели прочие науки, в которые математические методы привнесены «извне». В немалой степени отставанию от зарубежного уровня математизации биомедицины в СССР способствовала и лысенковщина (см. нашу статью «Долгое прощание с лысенковщиной»). Приведённые выше аргументы проявляют себя и при рассмотрении ошибок, допускаемых при использовании ФА.

Основы ФА зародились в конце 19 века, когда Ф. Гальтон и К. Пирсон, работая с антропометрическими и психологическими данными, начали развивать идею латентных, генерализованных признаков. В 1901 г. К.Пирсон выдвинул эту идею, назвав его методом главных осей (компонент). Началом современного периода развития факторного анализа считают публикацию Ч. Спирмена « General intelligence objectively determined and measured» от 1904 г. Споры вокруг этой статьи продолжались не одно десятилетие. Впрочем, и современные, новые методы этого вида анализа, также вызывают не меньшие споры. Основная причина этих споров - отсутствие математической однозначности решения. Однако такая неоднозначность не является оправданием тех ошибок, о которых мы будем говорить ниже. Более того, поливариантность решений в ФА даёт возможность поиска такого решения, которое является наиболее логичным и интерпретабельным.

Перейдём непосредственно к технологии ФА. Под фактором понимается гипотетическая, непосредственно не измеряемая, латентная (скрытая) переменная, которая имеет линейные корреляционные связи с исходными измеряемыми переменными. Цели ФА могут быть различными, в зависимости оттого, какая из имеющихся техник применяется в том или ином конкретном случае. Одной из таких целей является выявление гипотетических (ненаблюдаемых) факторов, призванных достаточно полно объяснить корреляционную матрицу наблюдаемых количественных признаков. При этом предполагается, что наблюдаемые переменные в свою очередь являются линейной комбинацией факторов. Отметим, что по определению каждый из факторов непосредственно для измерения недоступен - он гипотетичен, и представляет собой не более чем сумму измеряемых количественных признаков с различными весовыми коэффициентами.

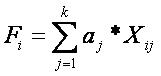
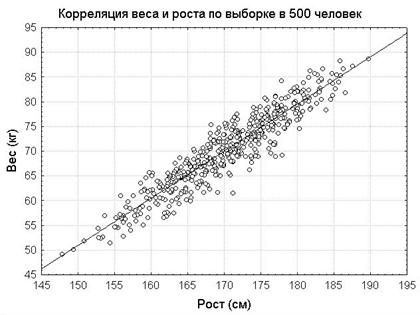
Такое выражение для ценки величины фактора может иметь, например, такой вид, представленный на формуле слева. При этом индекс « i» относится к номеру наблюдения (строке в матрице данных), а индекс « j» относится к номеру измеряемой переменной (столбцу в матрице данных). Индекс a j означает весовой коэффициент. Поскольку различие единиц измерений и масштаба измеряемых переменных могли бы оказывать влияние на величину такого коэффициента, то весовые коэффициенты вычисляются для так называемых безразмерных переменных. Процедура получения безразмерных переменных заключается в том, что для каждого значения количественных переменных в исходной матрице данных производится вычитание среднего значение (по данной конкретной переменной) и полученная разность делится на стандартное отклонение (для этой же переменной). Полученные таким образом безразмерные переменные имеют нулевое среднее и единичное стандартное отклонение. Итак, первое ограничение на использование факторного анализа заключается в том, что используемые в этом виде анализа признаки должны быть количественными. Далее, технология ФА построена на линейных соотношениях (корреляциях) между исходными количественными признаками. В качестве примера такой зависимости приведём двумерную диаграмму рассеяния, отражающую линейную корреляцию между ростом и весом человека.

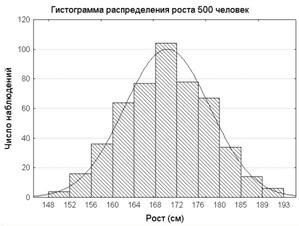
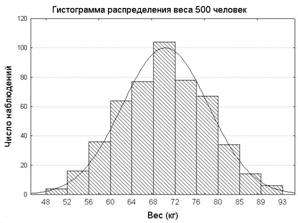
Отметим также, что процедура ФА использует корреляционную матрицу, состоящую из коэффициентов корреляции Пирсона. Вычисление же коэффициентов корреляции Пирсона предполагает, что каждый из анализируемых количественных признаков, подчиняется нормальному закону. Ниже приведены гистограммы распределения для роста и веса.

На этих двух рисунках сплошной чертой изображена кривая плотности нормального распределения. Проверка гипотезы нормальности также подтверждается с помощью критериев Шапиро-Уилки и Колмогорова-Смирнова.

Вернувшись к двумерной диаграмме рассеяния роста и веса, можно отметить, что рассеяние наблюдений имеет форму эллипса. Причём одна из осей этого эллипса, изображённая непрерывной прямой линией, гораздо длиннее той оси, которую можно провести перпендикулярно к первой оси. Это означает, что дисперсия наблюдений гораздо больше по первой оси, чем по второй. Фактически первая ось в данном случае выступает в роли первого фактора, как линейной комбинации двух количественных признаков, роста и веса.

Разумеется, для случая всего лишь двух признаков использование ФА лишено смысла. Одна из целей ФА является редукция (свёртка) пространства исходных признаков. Под редукцией понимается переход от многих исходных количественных признаков к пространству факторов, число которых значительно меньше числа исходных количественных признаков. Например, от исходных 20-40 количественных признаков производится переход к 3-5 факторам. Что же даёт исследователю уменьшение размерности признакового пространства? Почему целесообразно использовать такой переход? Попытаемся ответить на эти вопросы поподробнее.

Анализируемые в совокупности корреляционные коэффициенты отражают множество объективно существующих взаимосвязей, которые «зашумлены» большим количеством второстепенных, чаще всего не учитываемых, причин. Кстати, нередко в этом случае в качестве синонима термина причина используют и термин фактор, т.е. некая влияющая, действующая (на интересующий нас комплекс основных показателей) причина. В нашем контексте во избежание двусмысленности мы будем использовать термин «фактор» лишь в том смысле, как он первоначально определён выше. Неким аналогом такого неизмеряемого, а вычисляемого показателя, является индекс Кетле, вычисляемый с использованием роста и веса.

Технология ФА позволяет произвести некоторое разделение реальных взаимосвязей, и этого «шума». Такая «очищенная» от «шума» структура взаимосвязей позволяет сконцентрировать в некоторых из новых переменных - факторах, значительно больше информации, нежели в отдельно взятой исходной количественной переменной. Благодаря этому отдельный фактор можно рассматривать как совокупность наиболее сильно взаимосвязанных между собой исходных признаков. Вследствие этого ФА позволяет вычленить из всего многообразия исходных признаков отдельные конгломераты таких взаимосвязанных исходных признаков. Исходя из состава таких конгломератов, а также из величины весовых коэффициентов, возможно на вербальном уровне описать свойства такого фактора, связав его с соответствующим прилагательным (гормональный, спирометрический, гематологический, гуморальный, и т.п.). При этом оказывается, что отображение всех наблюдений в осях нескольких пар первых факторов, обычно это пары Ф1-Ф2, Ф1-Ф3, Ф2-Ф3 и т.п. (Ф i - i-тый фактор), даёт достаточно информативное представление о взаимном расположении сравниваемых многомерных групп наблюдений. Итак, с одной стороны выделение факторов позволяет выделить подгруппы взаимосвязанных количественных признаков, а с другой - более наглядно представить взаимное расположение имеющихся подгрупп наблюдений (состояние здоровья (здоров, болен), группы патологии, степень тяжести заболевания и т.п.) в осях этих новых, более информативных признаков.

Надо отметить, что разработано довольно много методик факторного анализа, в частности, так называемые техники R, Q, P, S, T и O. В биомедицине наибольший интерес представляет так называемая R-техника, в которой определяется взаимосвязь между признаками и факторами. Помимо этого имеется немало алгоритмов так называемого вращения осей, оценки первичных осей и т.д. В большинстве доступных современному исследователю статистических пакетах реализовано малая часть всех достижений ФА.

Ошибки использования ФА можно условно разделить на две части: ошибки применения и ошибки описания. В первом случае авторы достаточно подробно описывают процедуру ФА, не понимая при этом, что выполненный ими анализ ошибочен, поскольку авторская реализация противоречит основным положения ФА. Во втором случае авторы просто констатируют факт сам использования ФА, не сообщая читателю достаточной информации, необходимой для критической оценки надёжности описываемых выводов. Ясно, что в этом случае даже корректно выполненный ФА может не достичь своей цели, поскольку читатель не имеет возможности оценить по достоинству описанные результаты.

Если сделать в интернете поиск по ключевой фразе «Факторный анализ в медицине», то можно найти 2-3 десятка ссылок с материалами на эту тему. Сравнивая между собой публикации, найденные в результате такого поиска, можно отметить относительно полные описания ФА в работах С.Н. Поливода, А.А. Черепок. «Ремоделирование желудочков сердца и крупных сосудов у пациентов с гипертонической болезнью» (Запорожский государственный медицинский университет), Бенсбаа Абделькрим, «Факторная модель состояния осанки» (Черниговский государственный педагогический университет имени Т.Г. Шевченко), А.В. Черных, Ю.В. Малеев, Е.В. Левтеев, И.В. Аристов, В.А. Котюх «Новые подходы к исследованию антропометрических признаков шеи» (ВГМА им. Н.Н. Бурденко)

К большому сожалению, большая часть публикаций, в которых упоминается ФА, не позволяет читателю в полной мере оценить надежность, корректность и, соответственно, клиническую значимость описываемых результатов. В частности, большинство авторов просто умалчивают такие вопросы, как проверка линейности анализируемых взаимосвязей. Ничего не говорится о том, какой именно коэффициент корреляции (Пирсона или Спирмена) был использован в работе, проводилась ли проверка нормальности распределения и т.д. Нередко в таких работах просто декларируется сам факт использования ФА без всякой аргументации целесообразности этой технологии в описываемом исследовании. Типичные примеры таких публикаций «Факторный анализ кардиореспираторной заболеваемости населения Курской области» и «Значение нарушений диастолы левого желудочка при внесердечных оперативных вмешательствах у онкологических больных, страдающих ишемической болезнью сердца» ("Кремлевская медицина. Клинический вестник" 2, 1999г. ). Кстати, во второй работе авторы использовали некий «метод-мутант», назвав его «регрессионно-факторный анализ», совершенно не раскрыв его суть. Вполне возможно, что никакого ФА авторы и не использовали, а была лишь обычная множественная регрессия.

Наиболее же нелепая ошибка в использовании ФА была обнаружена нами в диссертация на соискание ученой степени доктора медицинских наук "Клиническая оценка реакции нейтрофилов при острой пневмонии у детей" (диссертант - Климов В.В., специальность 14.00.09 - педиатрия, 14.00.36 - аллергология и иммунология. Томский медицинский институт, Томск - 1989г. Незадачливый диссертант использовал для ФА такие признаки, как «Аномалии иммунитета», «Стигмы дисэмбриогенеза», «Аллергические диатезы», «ЧРЗ (частые респираторные заболевания)», «Хронические очаги в носоглотке», «Паразитарные инвазии», «Преморбидный фон (без иммунопатологии)», «Аллергические реакции», «Этиология (возбудитель)», «Неблагоприятное микросоциальное окружение» и т.п., которые по своей природе не являются измеряемыми, количественными показателями. В самой диссертации эти признаки представлены как альтернативные, дискретные признаки, т.к. качественные признаки. Использование дискретных, номинальных признаков для проведения ФА подобно тому, как если бы провести операцию сложения кислого с круглым, далее с зелёным, и затем вычесть из полученной суммы гинеколога, а результат умножить на физику. Подобные манипуляции напоминают усилия учёных-лапутян из "Путешествие Гулливера" Дж. Свифта по извлечению из огурцов солнечных лучей, пережиганию льда в порох, и усилия «знаменитого медика, особенно прославившегося лечением этой болезни путем двух противоположных операций, производимых одним и тем же инструментом» описанных автором в пятой главе третьей части «Путешествие в Лапуту, Бальнибарби, Лаггнегг, Глаббдобдриб и Японию» .

Итак, ФА является не только мощным методом анализа структуры взаимосвязей изучаемых объектов и признаков, но и сложным методом. Поэтому его реализация требует высокого уровня знаний и умений в этой специфичной области, что под силу лишь профессионалу-биостатистику.