О некоторых неиспользованных возможностях статистических методов в кардиологии

В.Ф. Фёдоров, А.В. Смирнов

НТЦ “МЕДАСС” г. Москва

При проведении исследований реакции сердечно-сосудистой и других систем организма человека на резкое изменение положения в пространстве (клино-ортостатическую пробу) среди других методов традиционно используют анализ динамики сердечного ритма. [см. напр. 7, 18, 26]

Анализируя работы последних лет по различным аспектам изучения сердечного ритма, как в норме, так и при многих патологиях, мы обратили внимание на явную тенденцию к уменьшению использования математического аппарата статистики.

Значительное количество исследователей применяют спектральные методы анализа изменчивости частоты сердечного ритма [см., например, 2, 4, 6, 9, 12, 14, 16, 17, 19, 24, 25, 27]. При этом, как правило, применяется процедура быстрого преобразования Фурье, из которой получают соотношения мощностей различных участков амплитудного спектра. Не останавливаясь на нереализованных возможностях спектральных методов (т.к. это не входит в задачу настоящей публикации), отметим, что количество используемых при этом параметров на порядки меньше числа состояний, которые авторам хотелось бы идентифицировать с их помощью. Иначе говоря, пространство используемых признаков, по нашему мнению, недостаточно для формирования образов, позволяющих идентифицировать многие из искомых состояний.

Несмотря на традиционную осторожность медицинской науки по отношению к применению новых математических подходов в диагностических целях, появляется всё больше работ по применению методов нелинейной динамики как при моделировании работы сердечно-сосудистой системы, так и непосредственно в диагностических целях [3, 5, 8, 10, 11, 13, 15, 20-23]. Не отрицая привлекательности и перспективности нового направления, хотелось бы отметить, что между математическими образами, получаемыми методами нелинейной динамики и физиологической (патофизиологической) интерпретацией в сознании подавляющего большинства исследователей, работающих не только в практической, но и в экспериментальной медицине, лежит глубокая пропасть.

В то же время, исследование сердечного ритма и его вариабельности (ВСР) в клинических целях приобретает всё большее значение, и даже встречаются утверждения, что “В настоящее время определение ВСР признано наиболее информативным неинвазивным методом количественной оценки вегетативной регуляции сердечного ритма”. [1]. В этой же работе приводятся стандарты на обработку сердечного ритма, принятые рабочей группой Европейского общества кардиологии и Североамериканского общества кардиостимуляции и электрофизиологии в 1994 году.

Не подвергая сомнению обоснованность всех вышеупомянутых подходов, авторы настоящей публикации предполагают, что существует физиологически и математически обоснованная возможность значительного расширения пространства признаков, содержащихся в хронокардиографическом сигнале. При этом достаточно использования обычных статистических алгоритмов, и их применение позволит существенно расширить методическую базу функциональной диагностики.

Нами применён алгоритм оценки состояния сердечно-сосудистой системы на основе анализа относительных приращений длительностей кардиоциклов.

Работа с относительными приращениями методом скользящего окна позволяет не только получить более корректные вторичные показатели, оценивающие уровень напряжённости регуляторных и исполнительных механизмов, но и существенно расширить пространство первичных статистических параметров для использования в дальнейших расчётных процедурах (например, методах распознавания образов).

Применённый нами алгоритм первичной статистической обработки относительных приращений длительностей кардиоциклов выглядит следующим образом.

1) Скользящим окном в 200 кардиоциклов производится статистическая обработка последовательности RR-интервалов в следующем порядке:

превратить ряд интервалов в ряд их относительных приращений:

t _n=(lgT_n-lgT_n-1) или t _n=lg(T_n/T_n-1), где T_n - это длительность кардиоцикла с номером n, а t _n - его относительное приращение по сравнению с предыдущим;

b) все значения относительных приращений, попавшие в окно, делятся на положительные и отрицательные,

c) внутри окна вычисляются статистические характеристики отдельно для положительных и отрицательных приращений:

математическое ожидание (M),

среднеквадратичное отклонение (s ),

коэффициент асимметрии (“скошенность”) - (g ₁),

коэффициент эксцесса (“обострённость”) - (g ₂),

мощность полураспределения (доля относительных приращений, попавшая в данный квадрант);

d) вычисляется для каждого полураспределения “интегральный показатель”:

;

2) Пункт 1) выполняется со сдвигом окна в 20 кардиоциклов (сдвиг - параметр, выбираемый из предполагаемой скорости изменения состояния испытуемого).

Количественные значения, приведённые в алгоритме, являются результатом определённого компромисса.

С одной стороны, применимость статистических методов зависит от мощности выборки (что следует из теоремы Гливенко - Кантелли). Следовательно, необходимо увеличивать размер скользящего окна для повышения математической корректности процедур и построенных на них оценок.

С другой стороны, при пульсе 60 ударов в минуту, 100 кардиоциклов соответствуют более чем полутора минутам, а 200 - трём с третью. При проведении же клино-ортостатической функциональной пробы-нагрузки основной переходный процесс может закончиться за две-три минуты. И за это время артериальное давление может резко упасть и снова возрасти до нормы, т.е. функциональное состояние, оцениваемое по статистическим параметрам, радикально изменится дважды. Следовательно, необходимо уменьшать размер скользящего окна для повышения физиологической корректности методики оценки функционального состояния, построенной на предложенных статистических параметрах.

“Интегральный показатель” - вычисляемая величина с размерностью частоты. Она введена нами после выявления тенденции противоположной направленности изменения величин “M”и “s ” при переходных процессах (изменении уровня нагрузки или её отмене). Поведение этого показателя в ходе нагрузки более “гладкое”, чем первичных показателей классической статистики и хорошо коррелирует с уровнем нагрузки. В процессе засыпания и при отдыхе после тяжёлой нагрузки он существенно снижается. Разница показателей положительной и отрицательной полуплоскостей указывает на направление динамики регуляции сердечного ритма (напряжение/расслабление). Соответственно, эти показатели могут быть названы “Индексом напряжения” (для отрицательных приращений) и “Индексом расслабления” (для положительных приращений).

У практически здорового человека с сохранными адаптационными механизмами сам процесс адаптации к функционированию в условиях допустимых физических, психических и/или интеллектуальных нагрузок проходит в виде квазилинейного нарастания соответствующих функций при нарастании нагрузок.

Линейная зависимость в координатах "нагрузка-реакция" нарушается только в областях неощутимых (допороговых) и экстремальных нагрузок (исчерпание резервов адаптации).

Суммарная кривая "нагрузка-реакция" (см. рис. 1) представляет собой S-образную зависимость (логисту), широко известную по описанию реагирующих систем [денситограммы в фотографии, нагрузочные кривые усилительных элементов (радиоламп или транзисторов) в электронике и т.п.].

На изображённой кривой можно выделить пять участков:

участок 0A - зона ареактивности, когда нагрузка настолько незначительна, что реагирование нецелесообразно,

участок AB - начальный нелинейный участок реагирования, когда с ростом нагрузки удельная реакция прирастает (может аппроксимироваться степенными или экспоненциальными функциями),

участок BC - зона линейного регулирования, когда прирост реакции пропорционален приросту нагрузки,

участок CD - конечный нелинейный участок, когда реагирующая система приближается к исчерпанию ресурсов адаптации,

участок правее D - уровень исчерпания ресурсов реагирования.

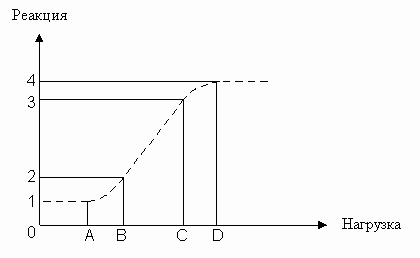
Рис. 1. Типовая кривая реагирования на нагрузку для различных реагирующих систем. Пояснения в тексте.

Очевидно, что при описании отдельных систем и/или органов организма человека характер нагрузки и параметры реагирования могут изменяться. Возможны специфические нагрузки, влияющие на отдельные параметры организма (например, влияние освещённости на диаметр зрачка), или универсальные, в ответ на которые изменяются параметры всех или большинства органов и систем (как, например, при гипоксии).

Параметры реакции не обязательно должны быть первичными (измеряемыми непосредственно). В качестве таковых могут использоваться результаты математической обработки временных рядов отдельных первичных параметров или различные математические комбинации нескольких параметров, характеризующих определённую структуру или функцию организма человека. Основные требования при выборе параметров - параметр, отображающий реакцию, должен при росте нагрузки изменяться логистически и соответствовать изменению физиологической функции.

На данной плоскости поведение объекта изучения может быть отображено четырьмя точками с координатами A1, B2, C3 и D4. Эти координаты не являются раз и навсегда зафиксированными величинами. При снижении адаптированности сузится зона ареактивности, возрастёт крутизна линейного участка, снизится уровень исчерпания ресурсов. В результате все координаты кривой изменятся. При повышении адаптированности - произойдут обратные изменения. Следует отметить, что горизонтальный участок, находящийся правее точки D, может быть очень короток, т.к. при запредельных нагрузках наступает срыв адаптации или разрушение адаптационных механизмов. В некоторых частных случаях при увеличении нагрузки может вновь начаться рост реакции, за счёт включения дополнительного (резервного) механизма адаптации.

Для организма человека, и даже для отдельных его систем и органов, можно выстроить набор таких плоскостей реагирования, на каждой из которых будут отображаться отдельные адаптационные реакции. При этом крутизна и размах кривых на отдельных плоскостях не обязательно будут иметь сходный характер. В целостном организме слабость развития одних органов и/или систем может функционально компенсироваться повышением активности других. Отслеживая динамику изменения координат кривых на всех плоскостях одновременно, можно оценивать уровень здоровья человека в процессе любых нагрузок или просто как функции времени. Таким образом, можно построить систему интегральной количественной оценки как здоровья человека в целом, так и отдельных адаптационных механизмов.

Описанные нами индексы с достаточным уровнем приближения отображаются логистами. Применение описанного алгоритма в клино-ортостатических исследованиях может позволить выявить гораздо больше нюансов реакции организма человека на данную функциональную пробу - нагрузку, т.к. расширяется пространство количественных признаков (параметров) реагирования.

Как сказано выше, это - четыре первых момента статистических распределений (мода, стандартное отклонение, скошенность и эксцесс), а также мощность каждого из полураспределений и его интегральный показатель. Эти шесть параметров для каждого полураспределения должны быть вычислены в состоянии исходного покоя и в начальный период восстановления. Кроме того, в каждом из двух состояний вычисляется математическое ожидание длительности кардиоцикла в данном окне, отображающее уровень функционирования.

Очевидно, что применение методов многомерной статистики существенно уменьшит количество параметров для решения конкретной диагностической/прогностической задачи, оставив только информативные для конкретной ситуации. Однако прежде чем такое упрощение произойдёт, необходимо пройти стадию набора обучающих выборок и минимизации признакового пространства на основе валидных данных.

Литература

1. Родионов А. Клиническое значение исследования вариабельности сердечного ритма. http://infoart.apex.dp.ua/med/cons/texts/hrv.htm, 05.10.1997.

2. Altimiras-J; Feliu-M; Aissaoui-A; Tort-L. Computing heart rate variability using spectral analysis techniques: HRVUAB, a ready-to-use program. Comput-Appl-Biosci. 1994 Sep; 10(5): 559-62

3. Berger R.D., Rosenbaum D.S., Cohen R.J. Is the Power Spectrum of the QRS Complex Related to a Fractal His-Purkinje System? American Journal of Cardiology, 71, 430-433, 1993.

4. Bronner-F; Douchet-MP; Quiring-E; Charpentier-A; Vi-Fane-R; Eisenmann-B; Chauvin-M; Brechenmacher-C Evolution de la variabilite de la frequence cardiaque apres chirurgie cardiaque sous circulation extra-corporelle: pontages aorto-coronariens ou remplacements valvulaires aortiques. Ann-Cardiol-Angeiol-Paris. 1998 Oct; 47(8): 549-54

5. Buldyrev SV, Goldberger AL, Havlin S, Peng CK, Stanley HE, Stanley MH, Simons M. Fractal landscapes and molecular evolution: modeling the myosin heavy chain gene family. Biophys J 1993 Dec;65(6):2673-2679

6. Cavalcanti-S; Severi-S; Chiari-L; Avanzolini-G; Enzmann-G; Bianco-G; Panzetta-G Autonomic nervous function during haemodialysis assessed by spectral analysis of heart-rate variability. Clin-Sci-Colch. 1997 Apr; 92(4): 351-9

7. Clifton-GD; Harrison-MR; Wermeling-DP; Long-RA; Fleck-RJ; Rolleri-RL; Weller-S; Brown-AR; Welch-RM. Pharmacokinetics and pharmacodynamics of a new cardiotonic vasodilator agent, 349U85, in normal subjects. Clin-Pharmacol-Ther. 1994 Jan; 55(1): 55-63

8. Goldberger AL, West BJ. Fractals in physiology and medicine. Yale J Biol Med 1987 Sep;60(5):421-435

9. Harel-T; Gath-I; Ben-Haim-SA. System response of the sinoatrial node during vagal stimulation. Physiol-Meas. 1998 May; 19(2): 149-57

10. Hausdorff JM, Mitchell SL, Firtion R, Peng CK, Cudkowicz ME, Wei JY, Goldberger AL. Altered fractal dynamics of gait: reduced stride-interval correlations with aging and Huntington's disease. J Appl Physiol 1997 Jan;82(1):262-269

11. Hausdorff JM, Purdon PL, Peng CK, Ladin Z, Wei JY, Goldberger AL. Fractal dynamics of human gait: stability of long-range correlations in stride interval fluctuations. J Appl Physiol 1996 May;80(5):1448-1457

12. Ho KK, Moody GB, Peng CK, Mietus JE, Larson MG, Levy D, Goldberger AL. Predicting survival in heart failure case and control subjects by use of fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 1997 Aug 5;96(3):842-848.

13. Hughson RL, Yamamoto Y, McCullough RE, Sutton JR, Reeves JT. Sympathetic and parasympathetic indicators of heart rate control et altitude studied by spectral analysis. J Appl Physiol 1994,77:2537-2542

14. Janssen-MJ; Swenne-CA; de-Bie-J; Rompelman-O; van-Bemmel-JH. Methods in heart rate variability analysis: which tachogram should we choose? Comput-Methods-Programs-Biomed. 1993 Sep; 41(1): 1-8

15. Kaplan DT, Furman MI, Pincus SM. Techniques for analyzing complexity in heart rate and beat-to-beat blood pressure signals. Comput Cardiol 1990, 243-246.

16. Lipsitz LA, Hashimoto F, Lubowsky LP, Mietus J, Moody GB, Appenzeller O, Goldberger AL. Heart rate and respiratory rhythm dynamics on ascent to high altitude. Br Heart J 1995 Oct;74(4):390-396

17. Mainardi-LT; Bianchi-AM; Baselli-G; Cerutti-S Pole-tracking algorithms for the extraction of time-variant heart rate variability spectral parameters. IEEE-Trans-Biomed-Eng. 1995 Mar; 42(3): 250-9

18. Moiniche-S; Hjortso-NC; Blemmer-T; Dahl-JB; Kehlet-H. Blood pressure and heart rate during orthostatic stress and walking with continuous postoperative thoracic epidural bupivacaine/morphine. Acta-Anaesthesiol-Scand. 1993 Jan; 37(1): 65-9

19. Otsuka K, Nakajima S, Yamanaka T. Vagal tone and its association with a new index of heart rate variability called 1/f fluctuations. J Amb Mon 1994,7:213-218

20. Otsuka K, Yamanaka T, Kubo Y, Disruption of fractals of heart rate variability in different types of pathophysiological settings. J Amb Mon 1994, 7:219-224

21. Otsuka K., Cornйlissen G., Halberg F. Age, Gender and Fractal Scaling in Heart Rate Variability. Clinical Science 1997, 93, p. 299.

22. Otsuka K., Cornйlissen G., Halberg F. Circadian Rhythmic Fractal Scaling of Heart Rate Variability in Health and Coronary Artery Disease. Clinical Cardiology 1997, 20, p. 631.

23. Peng CK, Havlin S, Hausdorff JM, Mietus JE, Stanley HE, Goldberger AL. Fractal mechanisms and heart rate dynamics. Long-range correlations and their breakdown with disease. J Electrocardiol 1995;28 Suppl:59-65

24. Petelez-T; Sosnowski-M; Axenti-I. Gutron treatment of patients suffering from essential orthostatic hypotony. Part Two--Autonomic system investigation. Int-Angiol. 1993 Jun; 12(2): 138-44

25. Ramaekers-D; Ector-H; Vanhaecke-J; van-Cleemput-J; van-de-Werf-F Heart rate variability after cardiac transplantation in humans. Pacing-Clin-Electrophysiol. 1996 Dec; 19(12 Pt 1): 2112-9

26. Roose-SP; Glassman-AH; Attia-E; Woodring-S; Giardina-EG; Bigger-JT Jr. Cardiovascular effects of fluoxetine in depressed patients with heart disease. Am-J-Psychiatry. 1998 May; 155(5): 660-5

27. Speranza-G; Verlato-G; Albiero-A. Autonomic changes during pregnancy: assessment by spectral heart rate variability analysis. J-Electrocardiol. 1998 Apr; 31(2): 101-9